Let $w, d > 0$ and $\Delta \geq 4$ be integers. We wish to lower bound the number of port graphs of depth $d$, width $w$ and maximum degree $\Delta$. It is sufficient to consider a restricted subset of such port graphs, whose size can be easily lower bounded. We will count a subset of CX quantum circuits, i.e. circuits with only $CX$ gates, a two-qubit non-symmetric gate. Because we are using a single gate type, this is equivalent to counting a subset of port graphs with vertices of degree 4. Assume w.l.o.g that $w$ is a power of two. We consider CX circuits constructed from two circuits with $w$ qubits composed in sequence:

• Fixed tree circuit: A $\log_2(w)$-depth circuit that connects qubits pairwise in such a way that the resulting port graph is connected. We fix such a tree-like circuit and use the same circuit for all CX circuits. We can use this common structure to fix an ordering of the $w$ qubits, that refer to as qubits $1,\dots,w$.
• Bipartite circuit: A CX circuit of depth $D = d - \log_2(w)$ with exactly CX gates, each gate acting on a qubit and a qubit .

The following circuit illustrates the construction:

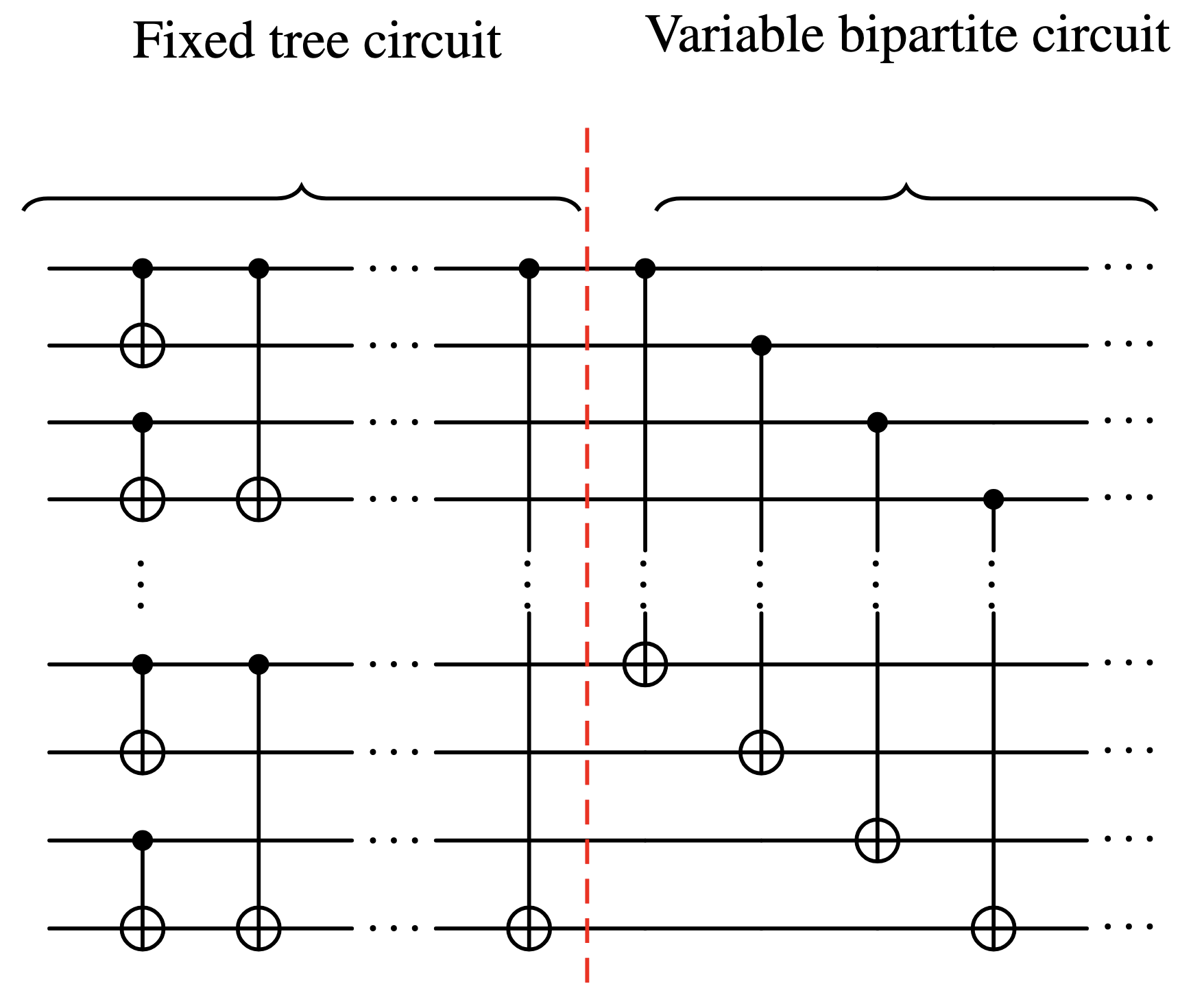
All that remains is to count the number of such bipartite circuits. Every slice of depth 1 must have $w / 2$ CX gates acting on distinct qubits. Every qubit $1$ to $w/2$ must interact with one of the qubits $w/2+1$ to $w$, so there are $(w/2)!$ such depth 1 slices. Repeating this depth 1 construction $D$ times and using Sterling’s approximation, we obtain a lower bound for the number of port graphs of depth $d$, width $w$ and maximum degree at least 4:

where we used $w = o(2^d)$ to obtain $\Theta(D) = \Theta(d)$ in the last step.